Spatial Smoothing using Network Analysis – Implementation

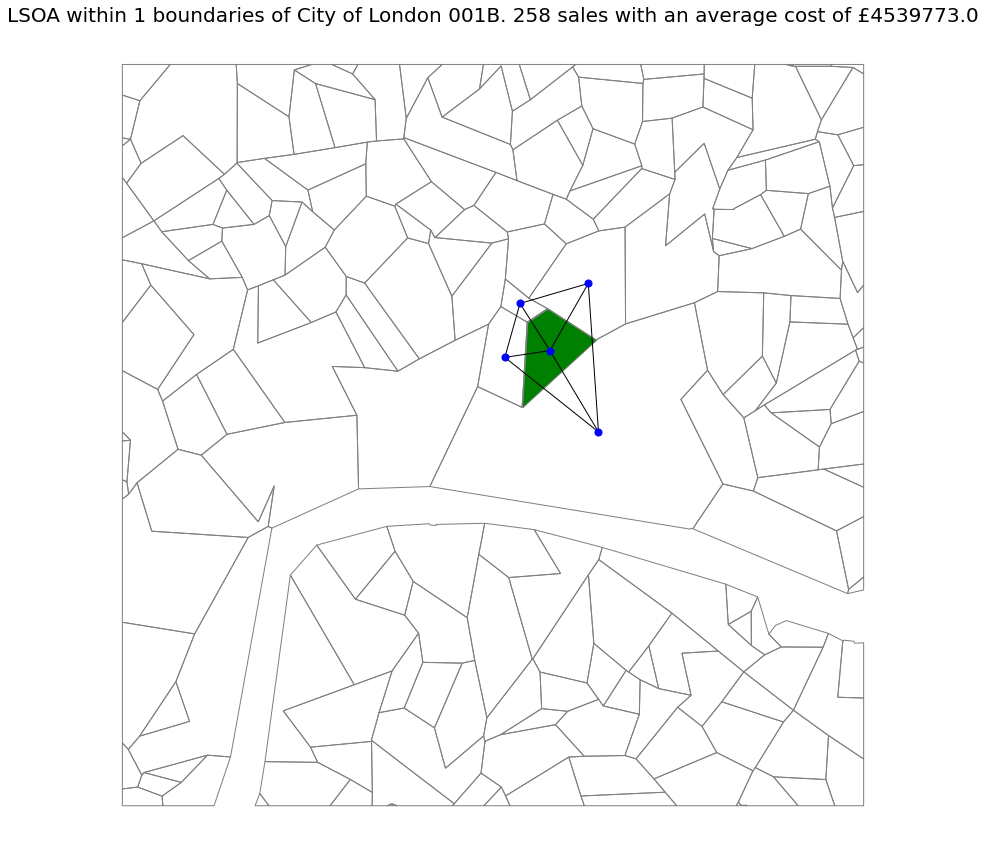
My previous post, network analysis and spatial smoothing, I investigated how to use NetworkX functions in python for potential use in spatial smoothing. In this post I’ll actually go over an example of the code being used to smooth average house price data across London. The code for this investigation is here

The area being used in this example is a a 5km square of London centered on St Paul’s Cathedral and the polygon’s are the 2011 census LSOAs.

The Plan:

1. Generate average price paid and number of sales in each LSOA
2. For a given LSOA find its neighbours
3. Aggregate the averages over the neighbourhood
4. Repeat 2 & 3 for all LSOAs

Easy!

There are some pretty pictures at the bottom to visualise what is going on in this code.

Step 1 – Generate average price data for each LSOA

At the moment we only have price paid data as points in a geopandas dataframe (gdf) and the LSOA polygons. We need to combine these two to get the average price paid for houses in each pandas dataframe. The house price points are in the gdf LReg and the prices in the field “Details_Float”.

#Add Sales and Average Cost for each LSOA

#Sales
LSOA["LReg_Sales"] = [np.count_nonzero(LReg.loc[LReg.within(poly_geom),"Details_Float"].to_numpy()) for poly_geom in LSOA.geometry]

#Average Cost
LSOA["LReg_AvCost"] = [np.sum(LReg.loc[LReg.within(poly_geom),"Details_Float"].to_numpy()) for poly_geom in LSOA.geometry]/LSOA["LReg_Sales"]

With a bit of list comprehension we now have two columns in the LSOA gdf. One for the average price and another for number of sales, we’ll need both later on for aggregation. Note that where possible I’m using numpy arrays, this really helps speed up the calculations over large datasets.

Step 2 – For a given LSOA find its neighbours

Use queen weights to make the network of neighbours. Then generate an ego graph for a given LSOA and output the nodes (LSOA names) in this network.

This is contained within 2 functions “create_network_from_shapes” and “witin_n_boundaries” the later being very simple

#Returns a sub network of the nodes within netowork_size edges of your stated node
def witin_n_boundaries(G, node_name, network_size):
    G_n = nx.ego_graph(G, node_name, network_size)
    in_network = list(dict(G_n.nodes()).keys())

    return G_n, in_network

The final function doesn’t need the graph to be output, it only needs the in_network list of nodes. Outputting the graph makes this into a useful function by itself allowing me to make ego graphs quickly.

Step 3 – Aggregate the averages over the neighbourhood

We now have a list of polygon names, and a gdf of sales and average cost for each of these. It’s just a short set of functions to aggregate this up and then combine into a single function with step 2

#Given a list of polygons in a given gdf, what is the average value in these polygons
def Average_In_Neighbourhood(shape_gdf, shape_list, count, average):
    new = shape_gdf[shape_gdf['Name'].isin(shape_list)].loc[:,[count, average]]
    sales = np.sum(new[count])
    Av_Cost = np.round(np.sum(new[count] * new[average])/ sales)
    return [sales, Av_Cost]

#Combine the above two finctions into a single function we can use in a list comprehension in the next function
def average_within_n_boundaries_sub(shape_gdf, G, node_name, count, average, network_size):
    G_n, in_network = witin_n_boundaries(G, node_name, network_size=network_size)
    count_mean = Average_In_Neighbourhood(shape_gdf, in_network, count, average)
    return count_mean

I was able to run a test at this point to see if the functions worked

Which it does

Step 4 – Repeat 2 & 3 for all LSOAs

Combine all of the above into a single function

#For a given set of boundary shapefiles with average and count variables contained within. Find the average value of within network_size boundaries of each polygon
def average_within_n_boundaries(shape_gdf, count, average, network_size):
    G, pos = create_network_from_shapes(shape_gdf)

    count_name = count + "_within_" + str(network_size) + "_boundaries"
    average_name = average + "_within_" + str(network_size) + "_boundaries"
    count_mean = pd.DataFrame([average_within_n_boundaries_sub(shape_gdf, G, x, count, average, network_size) for x in shape_gdf["Name"]], columns = [count_name, average_name])

    return count_mean

Then use list comprehension to apply this to all LSOA in our GDF

pd.concat([LSOA, average_within_n_boundaries(LSOA, "LReg_Sales", "LReg_AvCost", 1)], axis=1)

And that’s spatial smoothing using network analysis.