The Dog and the Duck (repost)

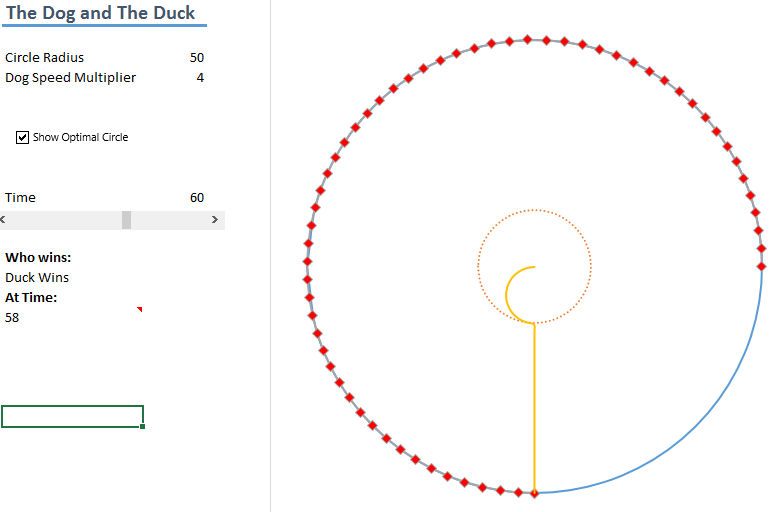
One of my friends sent me this puzzle from fivethirtyeight.com and here is my solution to how the dog needs to catch the duck.

There are a few key assumptions here that we can make from the beginning:

1. The duck is always travelling at its maximum speed: v
2. The dog always runs in the same direction at a constant speed: xv, where x is a constant
3. It gains nothing from changing directions
4. The function giving the dogs position is P(t)
5. So the dogs speed is given by $d/dt\left(P\right(t\left)\right)$
6. The function giving the ducks positon is Q(t)
7. The pool has radius R
8. The duck radial speed is always positive (it is always travelling towards the edge) and it never changes it’s rotational direction

For an excel version of the puzzle solution, look here

And some other notes about the solutions

I’ll be jumping between Cartesian coordinates (x,y) and polar coordinates (r,θ), probably using the notation

P= ar + bθ rather than brackets but I might change back

From here after a bit of thought we can see that the ducks path can be split into two parts

1. The period where the duck can remain on the opposite side of the pond to the dog. This is the case until the duck has a radial distance of$z$.
   • E.g. if $P\left(t\right)=ar+b\theta$then $Q\left(t\right)=cr+(b+\pi )\theta$
2. After this the duck needs to travel radially towards the dogs antipoint when the duck has a radial distance of $z$.

So the task now becomes: Find $z$

For this we don’t need to know the ducks path in part (1), although I will calculate it after I’ve found the solution to the first problem.

The dogs position can be given by $P\left(t\right)=Rr+kvt\theta ,$ focusing on the radial element, equating the different measures of the dog’s distance at time t (the angle at time t is $\varphi$)

$R\varphi =kvt,leta=\frac{kv}{R}\Rightarrow \varphi =at$

The radial distance of $z$ is reached when the radial part of the duck’s velocity becomes 0 and we know it’s total speed is $v$. We also. So the ducks Cartesian position is given by

$x=z\cos .\left(\varphi +\pi \right)=-zcos\left(at\right)andy=z\sin .\left(\varphi +\pi \right)=-zsin.\left(at\right)$

(the ducks angular position of $\varphi +\pi$ isn’t needed here but comes in useful later)

Differentiating these gives

$\frac{dx}{dt}=azsin\left(at\right)-\cos .\left(at\right)\frac{dr}{dt},and\frac{dy}{dt}=-azcost\left(at\right)-\sin .\left(at\right)\times \frac{dr}{dt}$

We know that $v^2={\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2$ therefore

$v^2=a^2{z}^2+{\left(\frac{dr}{dt}\right)}^2,\left(\frac{dr}{dt}\right)=0\Rightarrow v=az,a=\frac{kv}{R}\Rightarrow z=\frac{R}{k}$

At this point the duck now takes the quickest route to the edge towards the point directly opposite the dog. This radial distance $=R-z=\frac{R\left(k-1\right)}{k}$ at speed $v$. So it takes the time

$time=\frac{R\left(k-1\right)}{kv}$

The dog needs to travel a half circumference $R\pi$ at speed $kv$ so it takes time

$\frac{R\pi }{kv}$

Equating these gives

$\frac{R\pi }{kv}=\frac{R\left(k-1\right)}{kv}\Rightarrow k=\pi +1$

And that’s the solution to the problem $\pi +1.$

But I still want to know the ducks speediest path so I can plot it. The last bit is easy, the tricky bit is when the ducks radial distance is less than $z=\frac{R}{\pi +1}$.

What do we know? The duck’s angular velocity is the same as the dogs, in both cases it is kvt and we also know that the ducks Cartesian speed is v. So for function f(t) the ducks position is given by

$x=f\left(t\right)\cos .\left(kvt+\pi \right)=-f\left(t\right)\cos .\left(kvt\right)andy=f\left(t\right)\sin .\left(kvt+\pi \right)=-f\left(t\right)\sin .\left(kvt\right)$

Differentiating gives

$\frac{dx}{dt}=-f^{‘}\left(t\right)\sin .\left(kvt\right)-kvf\left(t\right)\cos .\left(kvt\right)$

$\frac{dy}{dt}=-f^{‘}\left(t\right)\cos .\left(kvt\right)+kvf\left(t\right)sin.\left(kvt\right)$

Squaring both and equating with v^2 gives the differential equation

$f^{‘}{\left(t\right)}^2=v^2(1-k^{2}f{\left(t\right)}^2)$

Solving this gives

$f\left(t\right)=\frac{\sin .\left(k\left(\pm v+c\right)\right)}{k}$ for some c

We know that at time t=0 that f’(t)=v and f(t)=0 which gives c=0 so

$f\left(t\right)=\frac{\sin .\left(kvt\right)}{k}$ and $f‘\left(t\right)=vsin\left(kvt\right)$

Done