In my posts on mapping so far I’ve focused on mapping points
This time I’ll be looking to generalise the last two points to polygons. i.e. can we find the distance from a point to the nearest polygon and the number of polygoins intersecting a circle of radius r around a point. All of this done in python using geopandas dataframes and spatial indicies.
I spend a long time trying to work this out myself. But in the end I had to ask the help of the author of this post and my functions are just his, but with minor tweeks. And I mean minor.
Concept
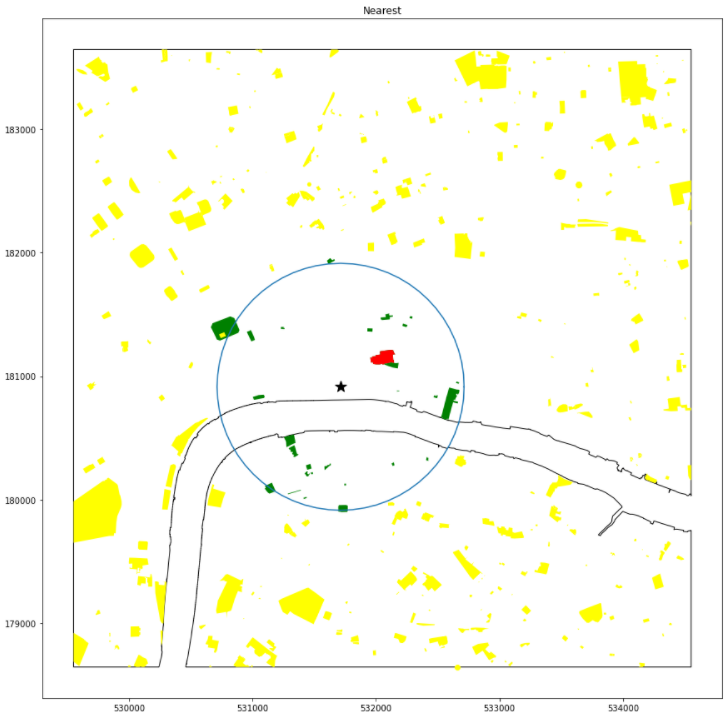
I have a point and a set of polygons. In this case I have a train station and all of the green spaces around St Pauls

I’m aiming to find the nearest green space to the star and it’s distance

I’ll use a spatial index to speed this process up a bit. This will limit the search to a radius of r around the point which will speed up the search

Options
The first option is to just find the distance from the point to all polygons then select the smallest of these values
poly.geometry.distance(point.geometry).min()This works for our small dataset, but will not scale well as both the point and the polygon counts increase.
Second option is to use a spatial index to extract the polygons within a radius then calculate the distances within this. This is the function I’ve taken from Shuai Zhou in the gps2space link above.
spatial_index = poly.sindex
bbox = point.geometry.buffer(1000, cap_style=3)
possible_matches_index = list(spatial_index.intersection(bbox.bounds))
poly.iloc[possible_matches_index].distance(point.geometry).min()This speeds the process up a lot as it reduces the number of calculations
Conclusion
This process works and does speed things up. But it is not quick.
In the nearest neighbour points test the calculation worked over two points dataframes with 1.4M points and calculated the nearest points within about a minute.
For the same set of points, and a smaller set of polygons this code takes over 20min. So more work is needed here